File:AnkiBasicExample3.png
AnkiBasicExample3.png (793 × 457 pixels, file size: 52 KB, MIME type: image/png)
Summary
Given: [$](\Omega,\mathcal{F},\mathbb{P})[/$] is a probability space [$]I[/$] is an index set with total order [$]\leq[/$] [$]\mathbb{F}=(\mathcal{F}_i)_{i\in I}[/$] is a filtration of the sigma algebra [$]\mathbb{F}[/$] [$](S,\Sigma)[/$] is a measurable space [$]X:I\times\Omega\rightarrow S[/$] is a stochastic process
If [$]X_i:\Omega\rightarrow S[/$] is a [$](\mathcal{F}_i,\Sigma)[/$]-measurable function, what is [$]X[/$] with respect to the filtration [$](\mathcal{F}_i)_{i\in I}[/$]?
X is an "adapted process" which is adapted to the filtration
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 13:47, 10 March 2023 | 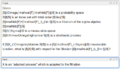 | 793 × 457 (52 KB) | Kevin Wang (talk | contribs) | Given: [$](\Omega,\mathcal{F},\mathbb{P})[/$] is a probability space [$]I[/$] is an index set with total order [$]\leq[/$] [$]\mathbb{F}=(\mathcal{F}_i)_{i\in I}[/$] is a filtration of the sigma algebra [$]\mathbb{F}[/$] [$](S,\Sigma)[/$] is a measurable space [$]X:I\times\Omega\rightarrow S[/$] is a stochastic process If [$]X_i:\Omega\rightarrow S[/$] is a [$](\mathcal{F}_i,\Sigma)[/$]-measurable function, what is [$]X[/$] with respect to the filtration [$](\mathcal{F}_i)_{i\in I}[/$]? X i... |
You cannot overwrite this file.
File usage
There are no pages that use this file.
